Structure Estimation for Discrete Graphical Models

Saturday. August 13, 2016 - 3 mins

Graphical models for high-dimensional data are used in many applications such as computer vision, natural language processing, bioinformatics, and social networks. Learning the edge structure of an underlying graphical model from the data is of great interest because the model may be used to represent close relationships between people in a social network or interactions between (ensembles of) neurons in the brain.

It has been well known that the inverse covariance matrix \((\Gamma=\Sigma^{-1})\) of any multivariate Gaussian is graph-structured as a consequence of Hammersley–Clifford theorem; zeros in \(\Gamma\) indicate the absence of an edge in the corresponding graphical model. For the non-Gaussian distributions, however, it is unknown whether the entries of \(\Gamma\) have any relationship with the strengths of correlations along edges in the graph. Loh and Wainwright [1] studied the analog of this type of correspondence for non-Gaussian graphical models, and we will touch base on the main theorem with a binary Ising model, which is a special case of the non-Gaussian.

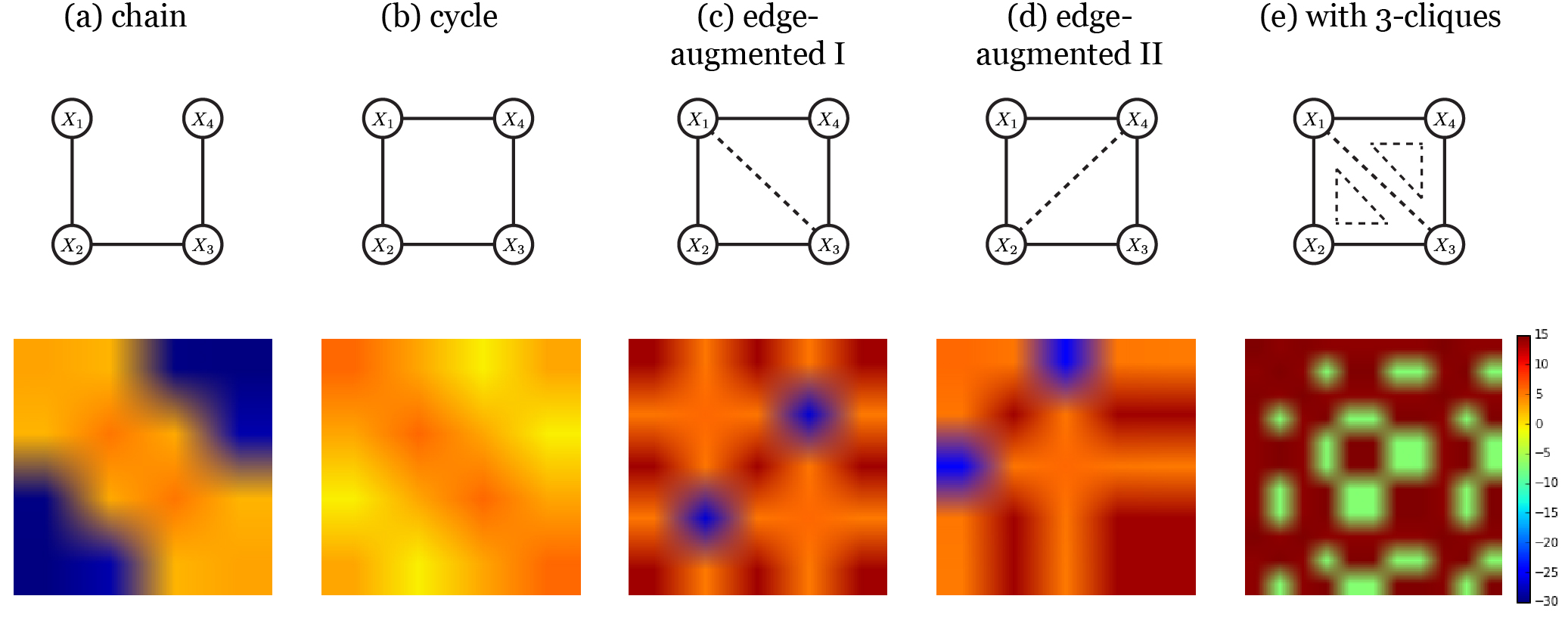
The figure above shows a simple graph on four nodes (row 1) and the corresponding \(\Gamma\) (row 2). Notably, the edge structure of the chain graph (a) is uncovered in

$$\Gamma_a = \Sigma_a^{-1} = \textrm{cov}(X_1,X_2,X_3,X_4)$$

where the edges (1,3), (1,4), and (2,4) are represented in blue colors implying (nearly) zero in \(\Gamma\) or no edges in the graph. Note that row 2 actually displays \(\log(\vert \Gamma \vert)\) to highlight the difference between zero and nonzero values in \(\Gamma\), and thus negative values (bluish and greenish color codes) in log domain suggest the absence of an edge due to finite precision of computations. The inverse covariance matrix \(\Gamma_b\) of the cycle (b), however, could not reveal its edge structure in the same way as the chain.

When do certain inverse covariances capture the structure of a graphical model? Here comes the main theorem:

THEOREM 1 (Triangulation and block graph-structure) Consider an arbitrary discrete graphical model of a general multinomial exponential family, and let \(\tilde{\mathcal{C}}\) be the set of all cliques in any triangulation of the graph \(G\). Then the generalized covariance matrix cov\((\Psi(X;\tilde{\mathcal{C}}))\) is invertible, and its inverse \(\Gamma\) is block graph-structured:

(a) For any subset \(A,B \in \tilde{\mathcal{C}}\) that are not subsets of the same maximal clique, the block \(\Gamma(A,B)\) is identically zero.
(b) For almost all parameters \(\theta\), the entire block \(\Gamma(A,B)\) is nonzero whenever \(A\) and \(B\) belong to a common maximal clique.

The essence of the theorem lies in adding higher-order moments into the original set of random variables to compute \(\Sigma\) through a certain rule stated above. Graphs in (c) and (d) are the examples of triangulation of the cycle in (b), and the set of all cliques \(\tilde{\mathcal{C}}\) of the triangulated graph (c,e) ends up with as follows:

$$\Psi(X) = \{ X_1,X_2,X_3,X_4,X_1X_2,X_2X_3,X_3X_4,X_1X_4,X_1X_3,X_1X_2X_3,X_1X_3X_4\}$$

Does the 11 \(\times\) 11 inverse of the matrix \(\textrm{cov}(\Psi(X))\) capture the aspects of the graph structure? Yes, greenish colors correspond to zeros in the inverse covariance, some of which are \((X_2,X_4),(X_2,X_3X_4), (X_2,X_1X_4)\). Furthermore, one of the corollaries says that a much smaller set of cliques may be sufficient to satisfy the theorem 1. Graphs (c) and (d) are the concrete examples of the corollary:

$$\Psi(X) = \{ X_1,X_2,X_3,X_4,X_1X_3\}$$

$$\Psi(X) = \{ X_1,X_2,X_3,X_4,X_2X_4\}$$

The two augmented vectors could unveil the absence of edges (1,3) and (2,4) respectively.

This is kind of cool because the authors have taken a leap toward making a general connection between graph structure and inverse covariance. Many remaining questions are expected to be solved such as how to deal with missing data or discrete graphical model with hidden variables.

[1] P. Loh and M.J. Wainwright.
Structure estimation for discrete graphical models: Generalized covariance matrices and their inverses.
Annals of Statistics, 41(6):3022–3049, 2013